Harmonising a Scale

It's almost impossible to overstate the importance of learning to harmonise a scale.

There are just so many advantages.

By learning this aspect of music theory, you can then:

1. harmonise an existing melody

2. compose music starting with chords (which can be way easier than starting with the melody especially for guitarists)

3. get to know the fretboard better

4. get to know barre chords better

5. increase your chord vocabulary (by playing chords like Am7b5)

6. understand how progressions work and how to improvise over them

There are many more benefits, but for now we are simply going to learn how harmony works and how to harmonise a major scale. This article assumes you know how to construct a major scale in terms of "whole, whole, half, whole, whole, whole, half." (If you don't, read my article "Constructing Major Scales" first.)

I. Definitions

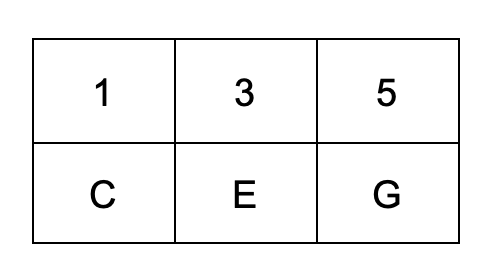
In general, our Western system of harmony is tertian meaning that it's built in 3rds. That means from any note in the scale, skip every other note to harmonize it. This can be done all the way out to 7 notes, but for our purposes we are going to limit the total number of notes to 3 which is a triad. In the key of C, for example, the scale is:

So if we take every other note to a total of 3 notes, that leaves us with:

Before we analyze this information, let's get a few definitions straight.

A whole step = 2 half-steps, and a half step is simply the distance between 2 adjacent notes. The following illustration of a piano keyboard can be helpful to see that the distance between C and C# is a half-step, and the distance between C# and D# is a whole-step.

Whether a chord is major or minor is determined by its 3rd. If the 3rd is two whole steps above the root, it's a major third. If the 3rd is a half-step lower, i.e. a whole plus a half step above the root, it's a minor third.

And in a major and minor triad, the 5th has to be "perfect." A perfect fifth is 7 half-steps above a root. If the fifth is flat, i.e. 6 half-steps above the root, it's called a diminished 5th.

If the fifth is sharp, i.e. 8 half-steps above the root, it's called an augmented 5th.

II. Analyzing Chords in the Major Scale

Let's go back to analyzing the harmonizing of the first note of the C major scale.

The distance between c and e is two whole steps so the 3rd is major. The distance between c and g is 7 half-steps so the 5th is perfect. The name of the chord is C major, or simply, C.

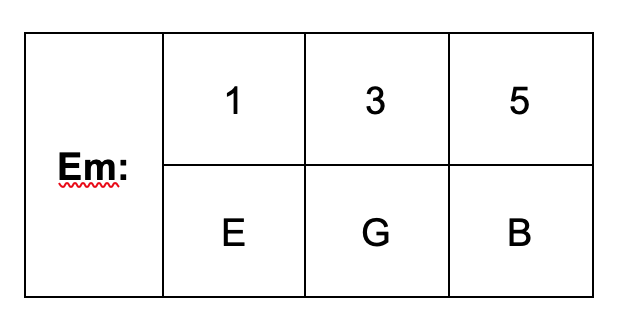
Now let's take the next scale degree in the key of C, i.e. the note d. Every other note would be

The distance between d and f is a step and a half (3 half-steps total) so the 3rd is minor. The distance between d and a is 7 half-steps so the 5th is perfect. The name of the chord is Dm.

Do yourself a huge favor and write out the rest of the scale on your own before reading on. You'll get so much more out of this if you do it yourself first, I guarantee it.

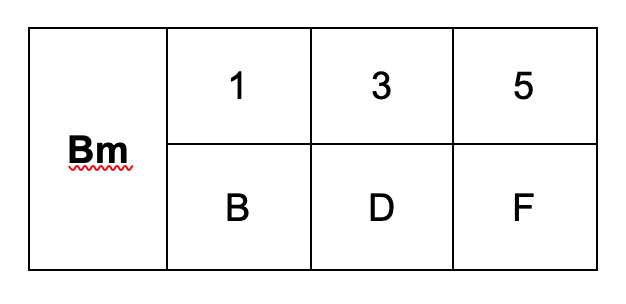
Your results should look like this:

The distance from b to d is 3 half-steps so the 3rd is minor. The distance from b to f is only 6 half-steps so, that makes the 5th diminished. A minor third and a diminished 5th is called a diminished triad.

Playing these chords on the guitar

Now try playing these chords on the guitar. If you have trouble playing any of them (especially the B diminished), consult your teacher.

Also harmonize the remaining keys of Db, D, Eb, E, F, F# or Gb, G, Ab, A, Bb, B. When it comes tomusic theory, there is no substitute for actually doing it.

Have fun with this!

About the author:

Dennis Winge is a professional guitarist living in New York with a passion for vegan food and bhakti yoga.

If you are interested in taking Guitar Lessons in Ithaca, NY, then be sure to contact Dennis!